Mystics & Statistics

A blog on quantitative historical analysis hosted by The Dupuy Institute

The U.S. Army Three-to-One Rule versus the 752 Case Division-level Data Base 1904-1991

Our most developed database through is our division-level database of 752 cases covering combat from 1904 to 1991. As this addresses modern combat, it is a useful database for such a test. Of those 752 cases, we have the forces ratios and outcome for 672 of them. All the engagements previously discussed from ETO in 1944 and Kharkov and Kursk in 1943 are drawn from this database. As such, there is some overlap between these 672 cases and the 116 cases from ETO and 73 cases from the Eastern Front previously used. The data shows a very clear pattern related to force ratios.

Division-level Engagements 1904-1991 (672 cases)

Force Ratio…………………..Percent Attacker Wins………………Number of Cases

0.20 to 0.20-to-1………………..0%………………………………………………….2

0.25 to 04.9-to-1………………22…………………………………………………….9

0.50 to 0.99-to-1………………42…………………………………………………..77

1.00 to 1.49-to-1………………55…………………………………………………150

1.50 to 1.99-to-1………………59…………………………………………………123

2.00 to 2.49-to-1………………71…………………………………………………..56

2.50 to 2.99-to-1………………83…………………………………………………..53

3.00 to 3.49-to-1………………69…………………………………………………..48

3.50 to 3.98-to-1………………77…………………………………………………..30

4.06 to 5.87-to-1………………65…………………………………………………..66

6.06 to 7.90-to-1………………88…………………………………………………..17

8.20 to 17.87-to-1……………100…………………………………………………..22

 

This table drives home in spades the problem with the U.S. Army current interpretation of the three-to-one rule (50% chance of defender success). To start with, the attacker starts winning over half the time at 1.00 to 1.49-to-1 odds. By the time they get to 2.50 to 2.99-to-1 odds they are winning 83% of the time. It is quite clear from this data that the U.S. Army rule is wrong.

Now, this data is skewed a little bit by the inclusion of engagements with “limited action” or only “limited attack.” They include engagements where the attacker has a significant force ratio but conducted only an initial probing attack of battalion size. Sometimes those attacks did not succeed. So the success rate of some the higher odds engagements would actually be higher if these were eliminated. So, we ended up culling 102 of these engagements from the above table to produce the following table.  There is not a big difference in the results between this tighter table of 570 cases and the previous table of 672 cases. The primary difference is that the attacker tends to be more successful in all categories. All the culled engagements were from World War II.

Division-level Engagements, 1904-1991 (570 cases) – culled data set

 

Force Ratio………………….Percent Attacker Wins……………….Number of Cases

0.20 to 0.20-to-1………………..0%…………………………………………………2

0.25 to 04.9-to-1………………25……………………………………………………8

0.50 to 0.99-to-1………………52…………………………………………………..62

1.00 to 1.49-to-1………………62…………………………………………………133

1.50 to 1.99-to-1………………66…………………………………………………108

2.00 to 2.49-to-1………………80………………………………………………….49

2.50 to 2.99-to-1………………83………………………………………………….48

3.00 to 3.49-to-1………………70………………………………………………….40

3.50 to 3.98-to-1………………76………………………………………………….29

4.06 to 5.87-to-1………………73………………………………………………….55

6.06 to 7.90-to-1………………88………………………………………………….17

8.20 to 17.87-to-1……………100………………………………………………….17

56.20-109.98-to-1……………100…………………………………………………..2

 

Needless to say, this tighter data set is even further biased against the published U.S. Army three-to-one rule.

The U.S. Army Three-to-One Rule versus 49 U.S. Civil War battles

From 1st Alabama Cavalry, USV website (www.1stalabamacavalryusv.com). Alexander Lawrence was from Fayette County, Alabama and fought for the Union with the 1st Alabama Cavalry

As the three-to-one rule of thumb appears to have evolved out of the American Civil War (although not as published in FM 6-0), then we should probably look at just our Civil War battles in our database.

Among those 243 cases are 49 cases from the American Civil War. As the three-to-one rule may have evolved from that experience, let us looking at just those cases:

 Force Ratio……………………Percent Attacker Wins……………….Number of Cases

0.44 to 0.48-to-1…………………0%………………………………………………3

0.53 to 0.97-to-1………………..18……………………………………………….11

1.00 to 1.47-to-1………………..36……………………………………………….14

1.53 to 1.96-to-1………………..25……………………………………………….12

2.10 to 2.31-to-1………………..50…………………………………………………6

3.00-to-1……………………….100…………………………………………………1

5.00-to-1……………………….100…………………………………………………1

15.05-to-1……………………..100…………………………………………………1

 

The American Civil War is a very good test case for such an examination. Both officer corps were primarily trained at West Point (the U.S. military academy); both armies fought in the same style and doctrine; they used most of the same weapons, including the same muskets and same artillery; they were similar in culture; and they were similar in training, doctrine, background and capability. While some historical mythology has tried to make the southern Americans better fighters, it is hard to accept the argument that a farmer from North Carolina is a different, more motivated or a more capable fighter than a farmer from Pennsylvania. Most of the United States was rural. There wre also units raised to fight for the north from all of the southern states. This is about an equal comparison between two opponents that one is going to find.

The end results from these two tests are that the three-to-one rule as recorded in FM 6-0 clearly does not apply. In the case of the Civil War data at 2.10 to 2.31-to-1 odds the attacker is winning half the time. Where does one get the notion that at 3.00-to-1 odds the defender will win half the time? What historical data established that?

So the U.S. Army version of the three-to-one (meaning defender wins half the time) does not show up in the almost 400 years of history that we are examining here and does not show up in the American Civil War.

Validating A Combat Model (Part XIII)

Gun crew from Regimental Headquarters Company, U.S. Army 23rd Infantry Regiment, firing 37mm gun during an advance against German entrenched positions, 1918. [Wikipedia/NARA]

[The article below is reprinted from June 1997 edition of The International TNDM Newsletter.]

The Second Test of the Battalion-Level Validation:
Predicting Casualties Final Scorecard
by Christopher A. Lawrence

While writing the article on the use of armor in the Battalion-Level Operations Database (BLODB), I discovered that l had really not completed my article in the last issue on the results of the second battalion-level validation test of the TNDM, casualty predictions. After modifying the engagements for time and fanaticism. I didn’t publish a final “scorecard” of the problem engagements. This became obvious when l needed that scorecard for the article on tanks. So the “scorecards” are published here and are intended to complete the article in the previous issue on predicting casualties.

As you certainly recall, amid the 40 graphs and charts were six charts that showed which engagements were “really off.” They showed this for unmodified engagements and CEV modified engagements. We then modified the results of these engagements by the formula for time and “casualty insensitive” systems, we are now listing which engagements were still “off” after making these adjustments.

Each table lists how far each engagement was off in gross percent of error. For example, if an engagement like North Wood I had 9.6% losses for the attacker, and the model (with CEV incorporated) predicted 20.57%, then this engagement would be recorded as +10 to +25% off. This was done rather than using a ratio, for having the model predict 2% casualties when there was only 1% is not as bad of an error as having the model predicting 20% when there was only 10%. These would be considered errors of the same order of magnitude if a ratio was used. So below are the six tables.

Seven of the World War I battles were modified to account for time. In the case of the attackers we are now getting results with plus or minus 5% in 70% of the cases. In the case of the defenders, we are now getting results of plus or minus 10% in 70% of the cases. As the model doesn’t fit the defender‘s casualties as well as the attacker‘s, I use a different scaling (10% versus 5%) for what is a good fit for the two.

Two cases remain in which the predictions for the attacker are still “really off” (over 10%), while there are six (instead of the previous seven) cases in which the predictions for the defender are “really off” (over 25%).

Seven of the World War II battles were modified to account for “casualty insensitive” systems (all Japanese engagements). Time was not an issue in the World War II engagements because all the battles lasted four hours or more. In the case of the attackers, we are now getting results with plus or minus 5% in almost 75% of the cases. In the case of the defenders, we are now getting results of plus or minus 10% in almost 75% of the cases. We are still maintaining the different scaling (5% versus 10%) for what is a good fit for the two.

Now in only two cases (used to be four cases) are the predictions for the attacker really off (over 10%), while there are still five cases in which the predictions for the defender are “really off” (over 25%).

Only 13 of the 30 post-World War II engagements were not changed. Two were modified for time, eight were modified for “casualty insensitive” systems, and seven were modified for both conditions.

In the case of the attackers we are now getting results within plus or minus 5% in 60% of the cases. In the case of the defenders, we are now getting results within plus or minus 10% in around 55% of the cases. We are still maintaining the different scaling (5% versus 10%) for what is a good fit for the two.

We have seven cases (used to be eight cases) in which the attacker‘s predictions are “really off” (over 10%), while there are only five cases (used to be 10) in which the defender‘s casualty predictions are “really off” (over 25%).

Repetitious Conclusion

To repeat some of the statistics from the article in the previous issue, in a slightly different format:

The U.S. Army Three-to-One Rule versus 243 Battles 1600-1900

Now, at the time I wrote War by Numbers, I was not aware of this sentence planted in FM 6-0 and so therefore did not feel a need to respond to the “3-to-1 rule.” It is a rule of thumb, not completely without value, that had been discussed before. I thought this issue was properly understood in the U.S. analytical and defense community, therefore I did not feel a need to address it further. It turns out that I do. So, let me take a moment to tap into our databases and properly address this using all the resources at my disposal.

First of all, The Dupuy Institute has a database of 243 engagements from 1600-1900 called the Battles Data Base (BaDB). These are almost all field battles, where the two sides deployed their forces of tens of thousands of people and resolve their dispute that day. Of the 243 battles, only 40 of them last longer than a day. The largest engagement has the attacker fielding 365,000 men (Leipzig, 1813) and the smallest engagement had the defender fielding but 350 men (Majuba Hill, 1881).

As this rule of thumb evolved out of the U.S. Civil War, then an examination of historical field battles from 1600-1900 is particularly relevant. Looking at the force ratio for these battles shows:

Force Ratio…………………..Percent Attacker Wins………………..Number of Cases

0.26 to 04.9-to-1………………54%……………………………………………13

0.50 to 0.98-to-1………………54………………………………………………81

1.00 to 1.47-to-1………………56………………………………………………71

1.50 to 1.96-to-1………………63………………………………………………38

2.00 to 2.44-to-1………………50………………………………………………16

2.58 to 2.94-to-1………………57………………………………………………..7

3.00 to 3.43-to-1…………….100………………………………………………..5

3.75 to 3.76-to-1………………..0………………………………………………..2

4.00 to 4.93-to-1………………75………………………………………………..4

7.78 to 16.82-to-1……………..67………………………………………………..6

 

The pattern here is not particularly clear, as low odds attack, where the attacker is outnumbered, succeed over half the time, as do attacks at higher odds. Some of this is due to the selection of battles, some of this is due to the lack of regular trained armies, and some of this is due to the attacker choosing to attack because they have advantages in morale, training, experience, position, etc. that outweigh the numbers. But, the argument that is made in FM 6-0 that based upon historical data at three-to-one odds the defender wins 50% of the time is clearly not shown. For example, in this data set there are 12 cases between the odds of 2.50 to 3.50-to-1. Of those 12 cases, the attacker wins in 9 of them (75%). The three cases where the defender wins are: 1) Battle of Buena Vista in 1847 where Santa Anna’s Mexican Army attacked Zachary Taylor’s American Army at 2.94-to-1, 2) Battle of Inkeman in 1854 where the Russian Army attacked the French and British armies in Crimea at 2.63-to-1, and 3) Battle of Belfort in 1871 where the French Army attack the German Army at 2.75-to-1. One could certainly argue that in these three cases, the defenders held advantages in training, experience and overall combat effectiveness.

Next post will address the 49 American Civil War battles in our database.

Validating A Combat Model (Part XII)

[The article below is reprinted from April 1997 edition of The International TNDM Newsletter.]

The Second Test of the TNDM Battalion-Level Validations: Predicting Casualties
by Christopher A. Lawrence

FANATICISM AND CASUALTY INSENSITIVE SYSTEMS:

It was quite clear from looking at the battalion-level data before we did the validation runs that there appeared to be two very different loss patterns, based upon—dare I say it—nationality. See the article in issue 4 of the TNDM Newsletter, “Looking at Casualties Based Upon Nationality Using the BLODB.” While this is clearly the case with the Japanese in WWII, it does appear that other countries were also operating in a manner that produced similar casualty results. So, instead of using the word fanaticism, let’s refer to them as “casualty insensitive” systems. For those who really need a definition before going forward:

“Casualty Insensitive” System: A social or military system that places a high priority on achieving the objective or fulfilling the mission and o low priority on minimizing casualties. Such systems lend to be “mission obsessive” versus using some form of “cost benefit” method of weighing whether the objective is worth the losses suffered to take it.

EXAMPLES OF CASUALTY INSENSITIVE SYSTEMS:

For the purpose of the database, casualty sensitive systems were defined as the Japanese and all highly motivated communist-led armies. These include:

  • Japanese Army, WWII
  • Viet Mihn
  • Viet Cong
  • North Vietnamese
  • Indonesian

We have included the Indonesians in this list even though it was based upon only one example.

In the WWII and post-WWII period, one would expect that the following armies would also be “casualty insensitive”

  • Soviet Army in WWII
  • North Korean Army
  • Communist Chinese Army in Korea
  • Iranian “Pasdaran“

Data can certainly be found to test these candidates.

One could postulate that the WWI attrition multiplier of 4 that we used also incorporates the 2.5 “casualty insensitive” multiplier. This would imply that there was only a multiplier of 1.6 to account for other considerations, like adjusting to the impact of increased firepower on the battlefield. One could also postulate that certain nations, like Russia, have had “casualty insensitive” systems throughout their last 100 years of history. This could also be tested by looking of battles over time of Russians versus Germans compared to Germans versus British, U.S. or French. One could easily carry this analysis back to the Seven Years’ War. If this was the case, this would establish a clear cultural basis for the “casualty insensitive” multiplier, but to do so would require the TNDM to be validated for periods before 1900. This would all be useful analysis in the future, but is not currently budgeted for.

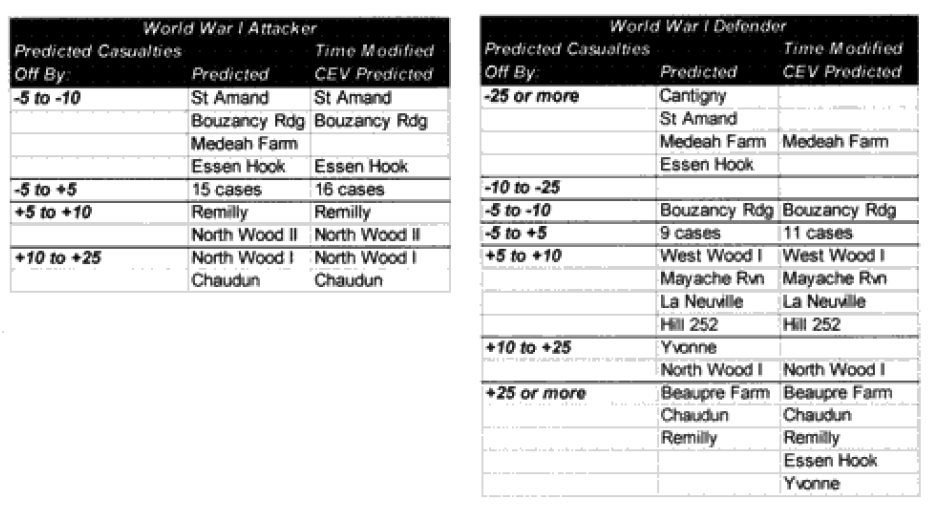
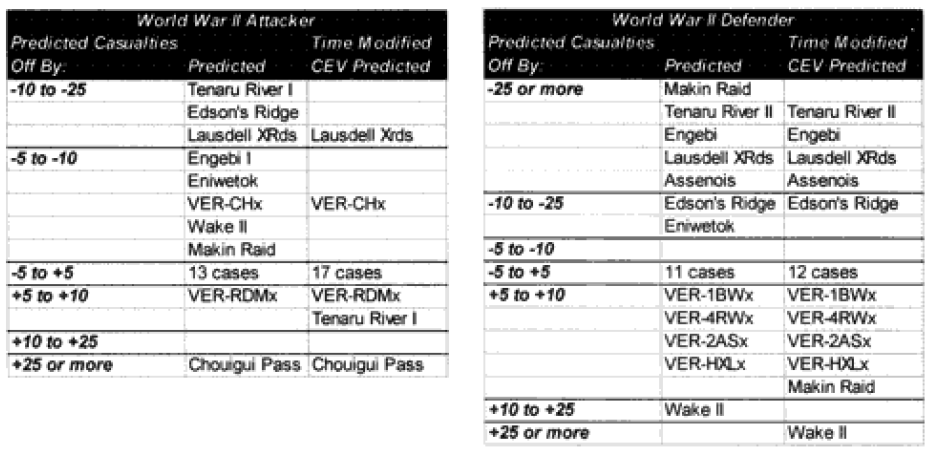
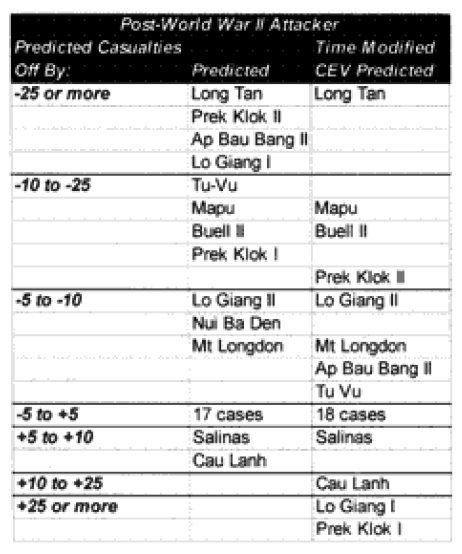
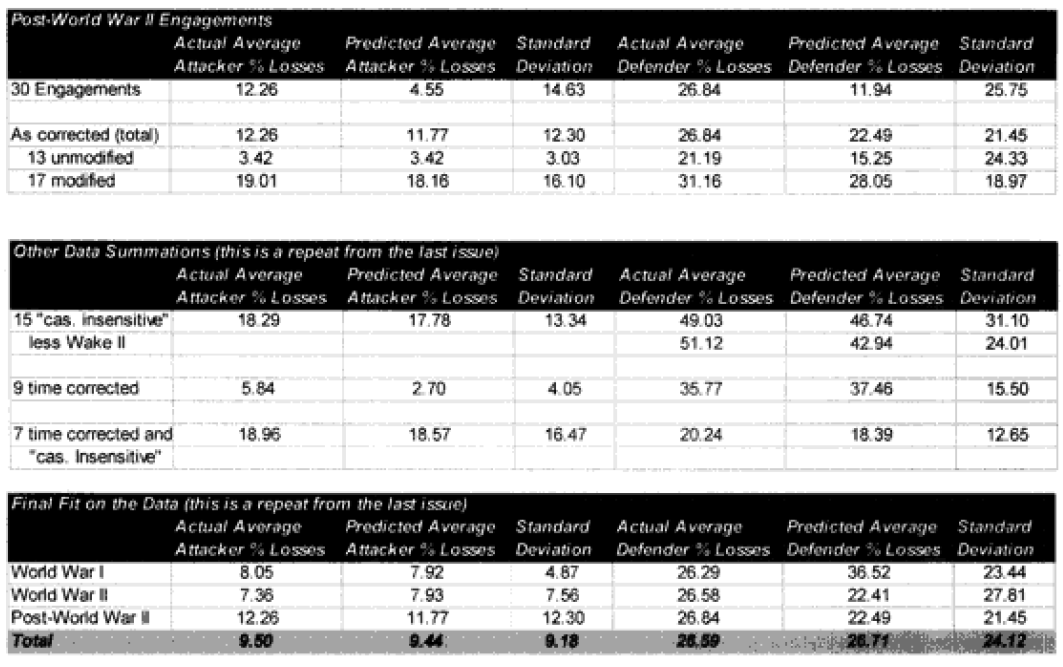
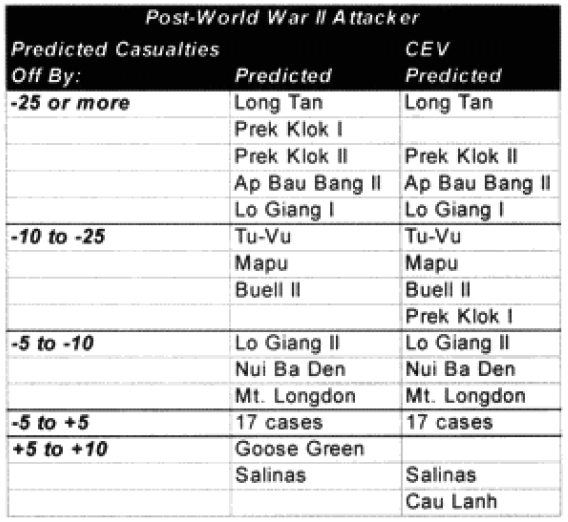
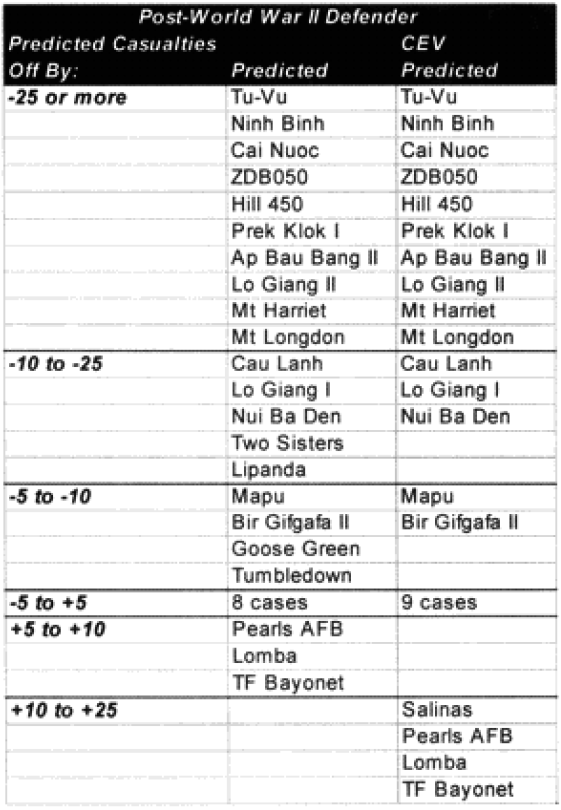
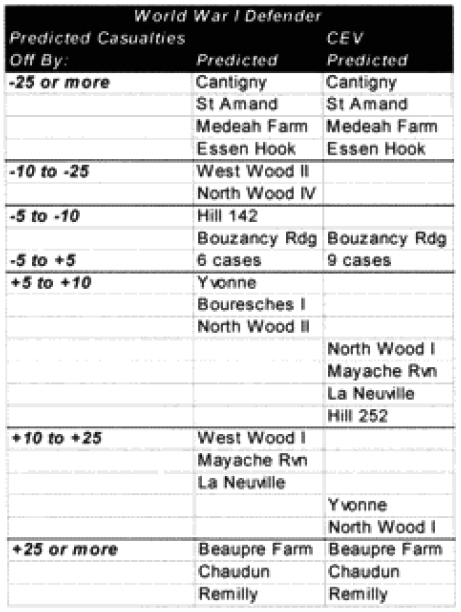
It was expected that the “casualty insensitive” multiplier of 2.5 derived from the Japanese data would be too high to apply directly to the armies. Much to our surprise, we found that this did not appear to be the case. This partially or wholly explained the under-prediction of the 15 of our 20 significantly under-predicted post-WWII engagements. Time would explain another one. And four were not explained.

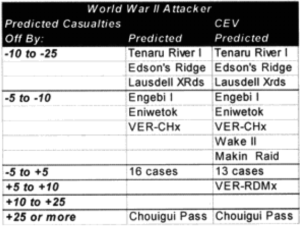
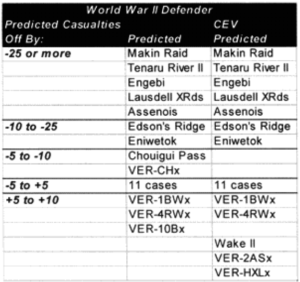
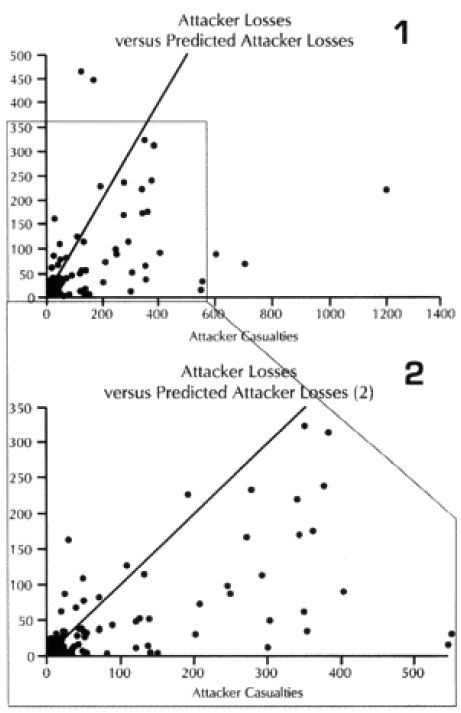
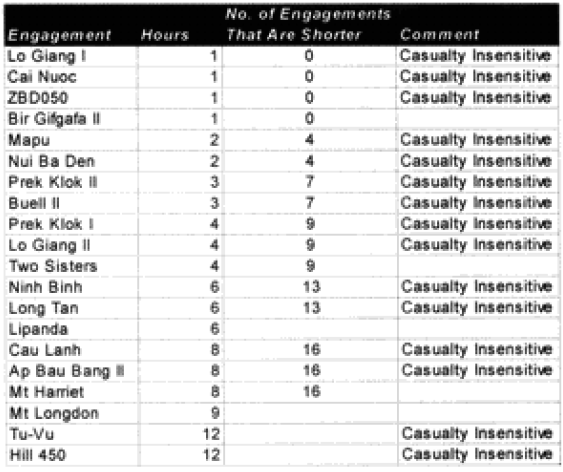The model noticeably underestimated all the engagements under nine hours except Bir Gifgafa I (2 hours). Pearls AFB (4.5) and Wireless Ridge (8 hours). It noticeably under-estimated all the 15 “fanatic” engagements. If the formulations derived from the earlier data were used here (engagements less than 4 hours and fanatic), then there are 17 engagements in which one side is “casualty insensitive” or in which the engagement time is less than 4 hours. Using the above formulations then 17 engagements would have their casualty figures changed.

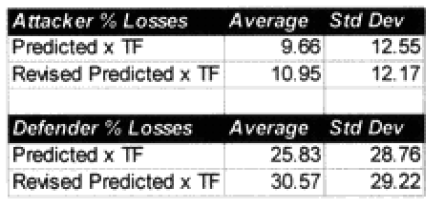
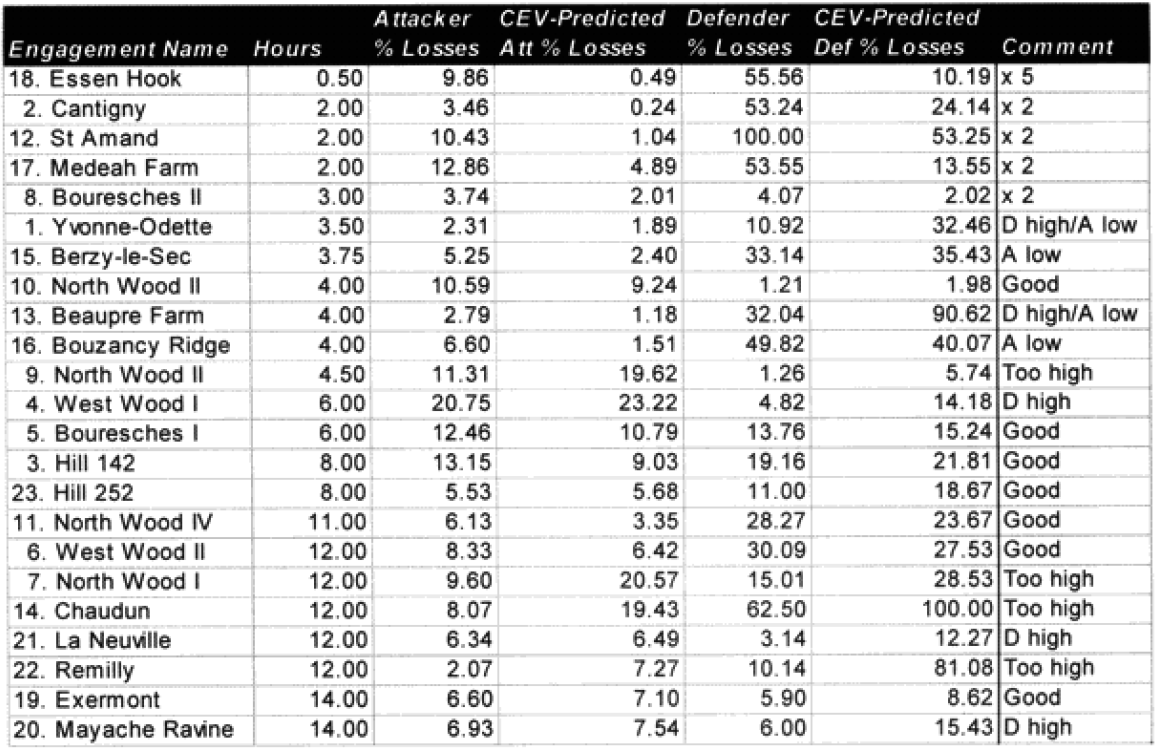
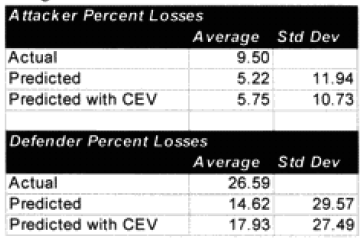
The modified percent loss figures are the CEV predicted percent loss times the factor for “casualty insensitive” systems (for those 15 cases where it applies) and times the formulation for battles less than 4 hours (for those 9 cases where it applies).

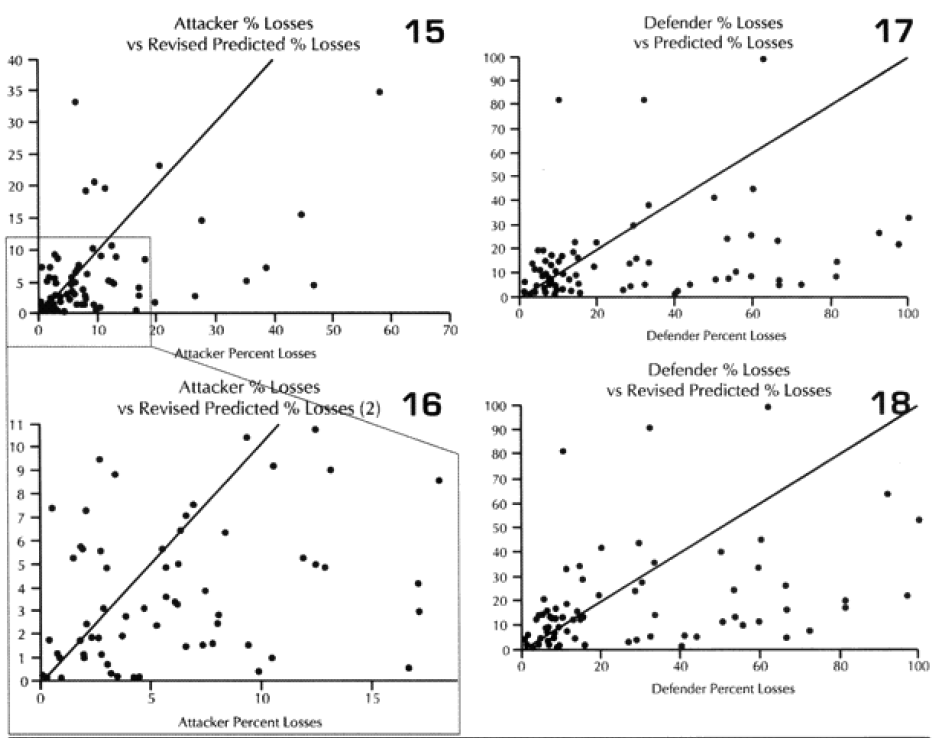
Looking at the table at the top of the next page, it would appear that we are on the correct path. But to be safe, on the next page let’s look at the predictive value of the 13 engagements for which we didn’t redefine the attrition multipliers.

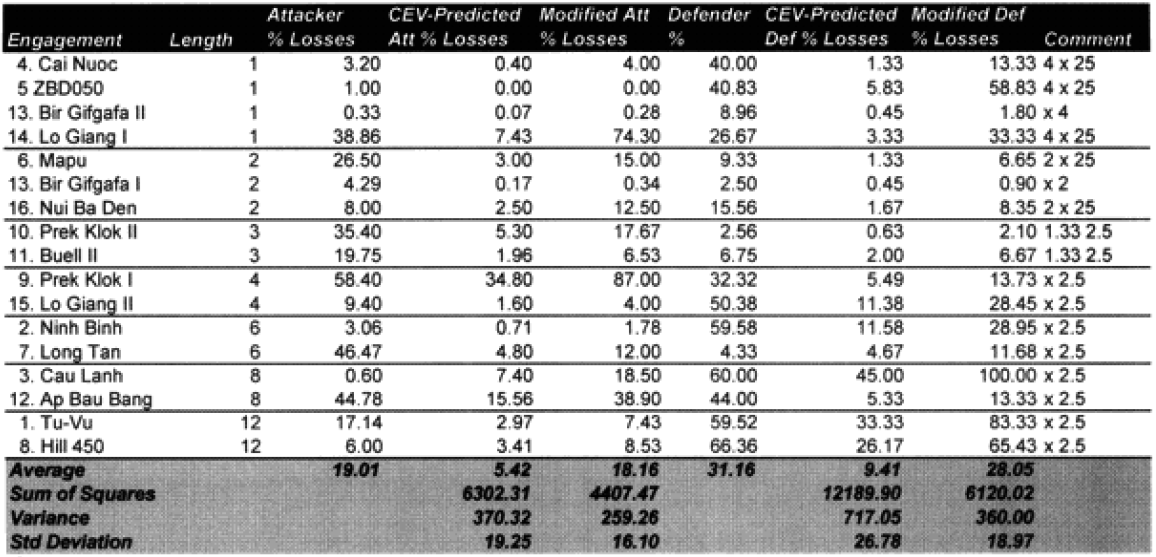The 13 engagements left unchanged:

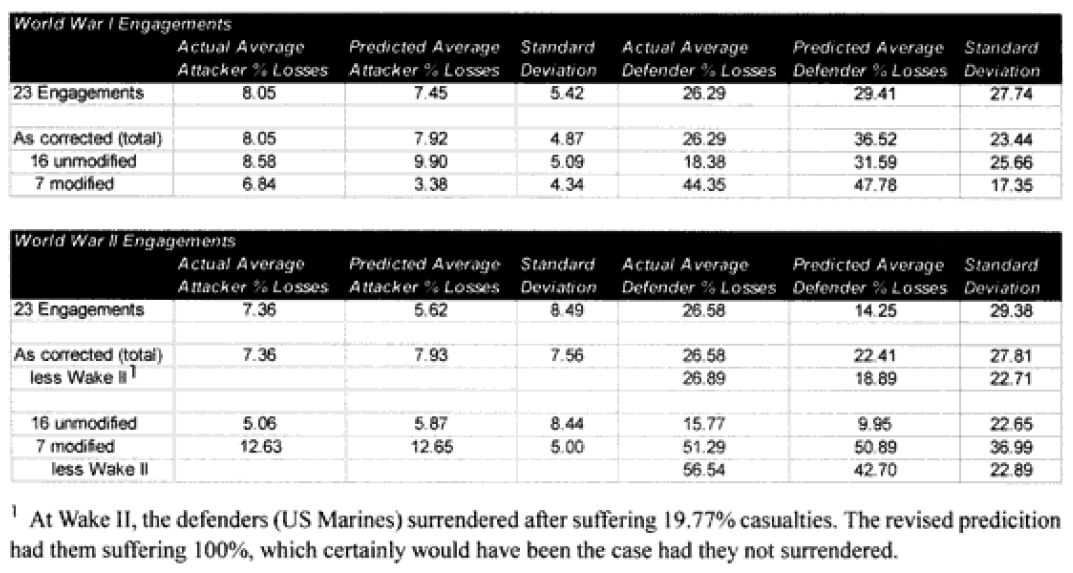
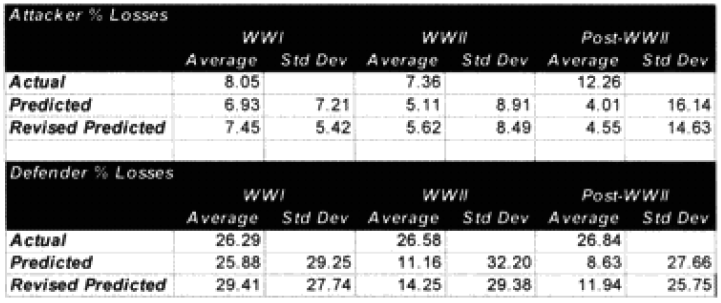
So, we are definitely heading in the right direction now. We have identified two model changes—time and “casualty insensitive.” We have developed preliminary formulations for time and for “casualty insensitive” forces. Unfortunately, the time formulation was based upon seven WWI engagements. The “casualty insensitive” formulation was based upon seven WWII engagements. Let’s use all our data in the first validation database here for the moment to come up with figures with which we can be more comfortable:

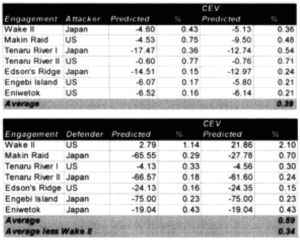
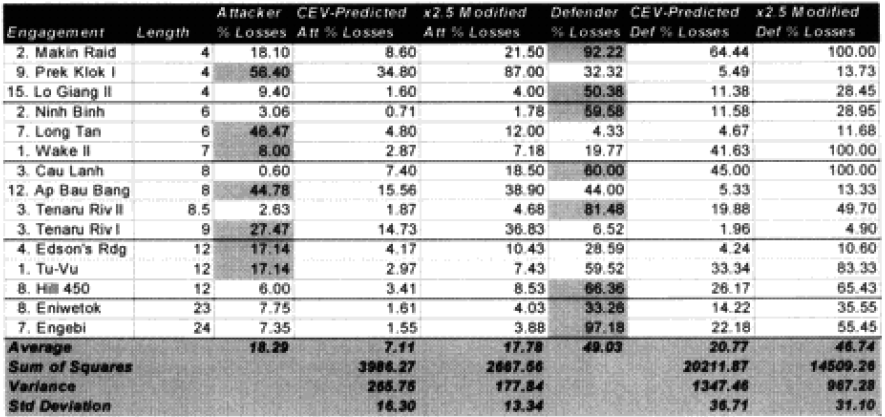The highlighted entries in the table above indicate “casualty insensitive” forces. We are still struggling with the concept that having one side being casualty insensitive increases both sides’ losses equally. We highlighted them in an attempt to find any other patterns we were missing. We could not.

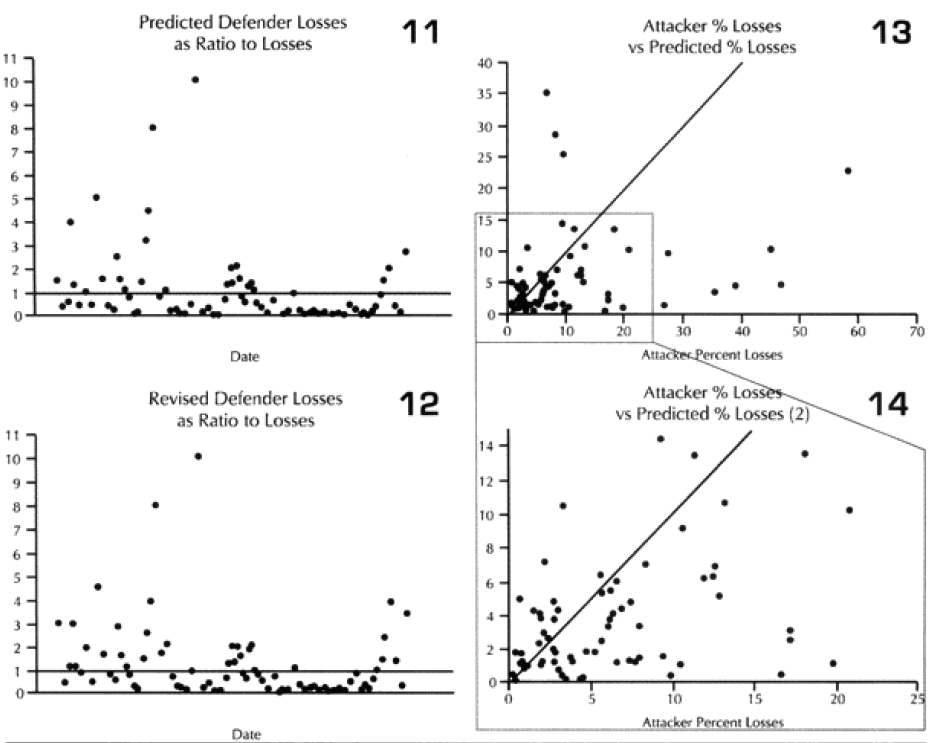
Now, there may be a more sophisticated measurement of this other than the brute force method of multiplying both sides by 2.5. This might include different multipliers depending on whether one is the fanatic vs non-fanatic side or different multipliers for attack or defense. First, I cannot find any clear indication that there should be a different multiplier for the attacker or defender. A general review of the data confirms that. Therefore, we are saying that the combat relationships between attacker and defender do not change in high intensity or casualty insensitive battles from those experienced in the norm.

What is also clear is that our multiplier of 2.5 appears to be about as good a fit as we can get from a straight multiplier. It does not appear that there is any significant difference between the attrition multiplier for types of “casualty insensitive” systems, whether they are done because of worship of the emperor or because the commissar will shoot slackers. Apparently the mode of fighting is more significant for measuring combat results than how one gets there, although certainly having everyone worship the emperor is probably easier to “administer.”

This still leaves us having to look at whether we should develop a better formulation for time.

Non-fanatic engagement of less than 4 hours: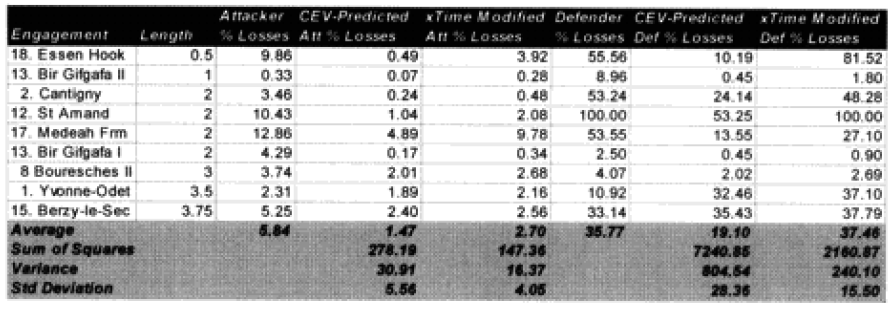

For fairly obvious reasons, we are still concerned about this formulation for battles of less than one hour, as we have only one example, but until we conduct the second validation, this formulation will remain as is.

Now the extreme cases:

List of all engagements less than 4 hours where one side was fanatic:

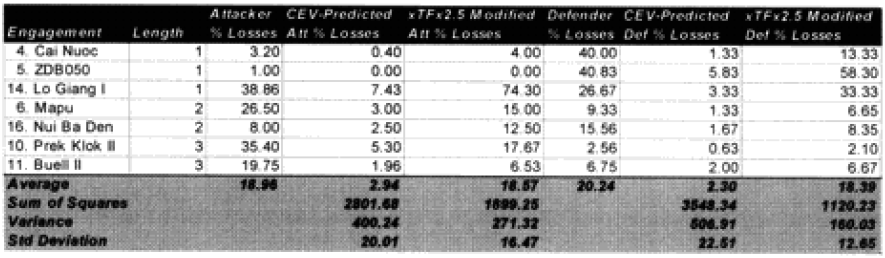It would appear that these formulations of time and “casualty insensitivity” have passed their initial hypothesis formulations tests. We are now willing to make changes to the model based upon this and run the engagements from the second validation data base to test it.

Next: Predicting casualties: Conclusions

The U.S. Army Three-to-One Rule

Various Three-to-one rules of thumbs have existed in the U.S. Army and in writings possibly as early as the American Civil War (1861-1865). These are fine as “rules of thumb” as long as one does not take them seriously and understands what they really mean. But, unfortunately, we have now seen something that is a loose rule of thumb turned into a codified and quantified rule. This is annoyingly overstating its importance and as given in U.S. Army manuals, is patently false.

The U.S. Army has apparently codified the “three-to-one rule” in its documentation and has given it a value. In the 2014 edition of FM 6-0, paragraph 9-103, it states that “For example, historically, defenders have over a 50 percent probability of defeating an attacking force approximately three times their equivalent strength.” This statement, on the surface, simply is incorrect. For example, the following table from my book War by Numbers is drawn from a series of 116 division-level engagements in France in 1944 against the Germans (see War by Numbers, page 10) They show the following relationship between force ratio and outcome:

European Theater of Operations (ETO) Data, 1944

 

Force Ratio………………..Result…………………Percent Failure…Number of cases

0.55 to 1.01-to-1.00………Attack Fails…………………..100%……………….5

1.15 to 1.88-to-1.00………Attack usually succeeds……21%………………..48

1.95 to 2.56-to-1.00………Attack usually succeeds……10%………………..21

2.71-to-1.00 and higher…Attacker Advances…………….0%……………….. 42

 

Now these engagements are from fighting between the U.S., UK and Germany in France and Germany in 1944. These are engagements between forces of roughly equal competence. As can be seen, based upon 42 division-level engagements, in all cases of attacks at three-to-one (more specifically 2.71-to-1 and greater), the attacker advanced. Meaning in all cases of attacks at three-to-one, the attacker won. This directly contradicts the statement in FM 6-0, and contradicts it based upon historical data.

This is supplemented by the following two tables on the next page of War by Numbers. The first table shows the German performance when attacking Soviet units in 1943.

Germans attacking Soviets (Battles of Kharkov and Kursk), 1943

 

Force Ratio………………..Result………………….Percent Failure…Number of cases

0.63 to 1.06-to-1.00………Attack usually succeeds……..20%……………………..5

1.18 to 1.87-to-1.00………Attack usually succeeds……….6%……………………17

1.91-to-1.00 and higher…Attacker Advances……………….0%……………………21

 

The next table shows the Soviet performance when attacking German units in 1943:

Soviets attacking Germans (Battles of Kharkov and Kursk), 1943

 

Force Ratio………………Result…………………..Percent Failure…Number of cases

0.40 to 1.05-to-1…………Attack usually fails…………70%……………………10

1.20 to 1.65-to-1.00…….Attack often fails…………….50%……………………11

1.91 to 2.89-to-1.00…….Attack sometimes fails…….44%……………………..9

 

These charts are from the fighting around Kharkov in February, March and August of 1943 and the fighting during the Battle of Kursk in July 1943. It is 73 engagements between the German and Soviet armies.

Now, there is a clear performance difference between the German and the Soviet armies at this time. This is discussed in considerable depth in War by Numbers and will not be addressed here. But, what it amounts to is that the German Army has an advantage in the casualty exchange and that advantage also shows up in the outcomes of the battles, as show above. If they attacked at two-to-one odds are greater, they would win. The Soviets attacking at the same odds would win only 56 percent of the time. Clearly, at the division-level, in a unit to unit comparison, the Germans were two or three times better than their Soviet opponents.

Still, even in the worse case, which is the Soviets attacking the Germans, we do not get to the claim made in FM 6-0, which is the defender won 50% of the time when attacked at three-to-one. In fact, the Soviets managed to win 50% of the time when attacking at 1.20 to 1.65-to-1. Something is clearly wrong with the statement in FM 6-0.

Now, at the time I wrote War by Numbers, I was not aware of this sentence planted in FM 6-0 and so therefore did not feel a need to respond to the “three-to-one rule.” It is a rule of thumb, not completely without value, that had been discussed before (see Dupuy, Understanding War, pages 31-37). I thought this issue was properly understood in the U.S. analytical and defense community, therefore I did not feel a need to address it further. It turns out that I do. So, I will take a moment to tap into our databases and properly address this using all the resources at my disposal. This will be in subsequent blog posts.

Validating A Combat Model (Part XI)

Dead Japanese soldiers lie on the sandbar at the mouth of Alligator Creek on Guadalcanal on 21 August 1942 after being killed by U.S. Marines during the Battle of the Tenaru. [Wikipedia]
[The article below is reprinted from April 1997 edition of The International TNDM Newsletter.]

The Second Test of the TNDM Battalion-Level Validations: Predicting Casualties
by Christopher A. Lawrence

SO WHERE WERE WE REALLY OFF? (WWII)

In the ease of the WWII results, we were getting results in the ball park in less than 60% of the cases for the attacker and in less than 50% of the eases in the case of the defenders. We were often significantly too low. Knowing that we were dealing with a number of Japanese engagements (seven), and they clearly fought in a manner that was different from most western European nations, we expected that they would be under-predicting, and some casualty adjustment would be necessary to reflect this.

We also examined whether time was an issue (it was not). The under-predicted battles are listed in the next table

We temporarily defined the Japanese mode of fighting as “fanaticism.” We decided to find a factor for fanaticism by looking at all the battles with the Japanese. They are listed below:

Looking at what multiplier was needed, one notes that .39 times 2.5 = .975 while .34 times 2.5 = .85. This argues for a “fanatic” multiplier of 2.5. The non-fanatic opponent attrition multiplier is also 2.5. There was no indication that both sides should not be affected by the same multiplier.

We had now tentatively identified two “fixes” to the data. l am sure someone will call them “fudges,“ but I am comfortable enough with the logic behind them (especially the fanaticism) that I would dismiss such criticism. It was now time to look at the modern data, and see what would happen if these fixes were applied to it.

SO WHERE WERE WE REALLY OFF? (Post-WWII)

A total of 20 battles were noticeably under-predicted. We examined them to see if there was a pattern in this under-prediction.

Next: “Casualty insensitive” systems

Validating A Combat Model (Part X)

French Army soldiers recover the dead from trenches during World War I [Library of Congress]

[The article below is reprinted from April 1997 edition of The International TNDM Newsletter.]

The Second Test of the TNDM Battalion-Level Validations: Predicting Casualties
by Christopher A. Lawrence

TIME AND THE TNDM:

Before this validation was even begun, I knew we were going to have a problem with the fact that most of the engagements were well below 24 hours in length. This problem was discussed in depth in “Time and the TNDM,” in Volume l, Number 3 of this newsletter. The TNDM considers the casualties for an engagement of less than 24 hours to be reduced in direct proportion to that time. I postulated that the relationship was geometric and came up with a formulation that used the square root of that fraction (i.e. instead of 12 hours being .5 times casualties. it was now .75 times casualties). Being wedded to this idea, l tested this formulation in all ways and for several days, I really wasn’t getting a better fit. All I really did was multiply all the points so that the predicted average was closer. The top-level statistics were:

TF=Time Factor

I also looked out how the losses matched up by one of three periods (WWI, WWII. and post-WWII). When we used the time factor multiplier for the attackers, the WWI engagements average became too high, and the standard deviation increase, same with WWII, while the post-WWII averages were still too low, but the standard deviations got better. For the defender, we got pretty much the same pattern, except now the WWII battles were under-predicting, but the standard deviation was about the same. It was quite clear that all I had with this time factor was noise.

Like any good chef, my failed experiment went right down the disposal. This formulation died a natural death. But looking by period where the model was doing well, and where it wasn’t doing well is pretty telling. The results were:

Looking at the basic results. I could see that the model was doing just fine in predicting WWI battles, although its standard deviation for the defenders was still poor. It wasn’t doing very well with WWII, and performed quite poorly with modem engagements. This was the exact opposite effect to our test on predicting winners and losers, where the model did best with the post-WWII battles and worst with the WWI battles. Recall that we implemented an attrition multiplier of 4 for the WWI battles. So it was now time to look at each battle, and figure out where were we really off. In this case. I looked at casualty figures that were off by a significant order of magnitude. The reason l looked at significant orders of magnitude instead of percent error, is that making a mistake like predicting 2% instead of 1% is not a very big error, whereas predicting 20%, and having the actual casualties 10%, is pretty significant. Both would be off by 100%.

SO WHERE WERE WE REALLY OFF? (WWI)

In the case of the attackers, we were getting a result in the ball park in two-thirds of the cases, and only two cases—N Wood 1 and Chaudun—were really off. Unfortunately, for the defenders we were getting a reasonable result in only 40% of the cases, and the model had a tendency to under-or over-predict.

It is clear that the model understands attacker losses better than defender losses. I suspect this is related to the model having no breakpoint methodology. Also, defender losses may be more variable. I was unable to find a satisfactory explanation for the variation. One thing I did notice was that all four battles that were significantly under-predicted on the defender sides were the four shortest WWI battles. Three of these were also noticeably under-predicted for the attacker. Therefore. I looked at all 23 WWI engagements related to time.

Looking back at the issue of time, it became clear the model was clearly under-predicting in battles of less than four hours. I therefore came up with the following time scaling formula:

If time of battle less than four hours, then multiply attrition by (4/(Length of battle in hours)).

What this formula does is make all battles less than four hours equal to a four-hour engagement. This intuitively looks wrong, but one must consider how we define a battle. A “battle” is defined by the analyst after the fact. The start time is usually determined by when the attack starts (or when the artillery bombardment starts) and end time by when the attack has clearly failed, or the mission has been accomplished, or the fighting has died down. Therefore, a battle is not defined by time, but by resolution.

As such, any battle that only lasts a short time will still have a resolution, and as a result of achieving that resolution there will be considerable combat experience. Therefore, a minimum casualty multiplier of 1/6 must be applied to account for that resolution. We shall see if this is really the case when we run the second validation using the new battles, which have a considerable number of brief engagements. For now, this seems to fit.

As for all the other missed predictions, including the over-predictions, l could not find a magic formula that connected them. My suspicion was that the multiplier of x4 would be a little too robust, but even after adjusting for the time equation, this left 14 of the attacker‘s losses under-predicted and six of the defender actions under-predicted. If the model is doing anything, it is under-predicting attacker casualties and over-predicting defender casualties. This would argue for a different multiplier for the attacker than for the defender (higher one for the attacker). We had six cases where the attacker‘s and defenders predictions were both low, nine where they were both high, and eight cases where the attackers prediction was low while the defender’s prediction was high. We had no cases where the attacker’s prediction was high and the defender’s prediction was low. As all these examples were from the western front in 1918, U.S. versus Germans, then the problem could also be that the model is under-predicting the effects of fortifications, or the terrain for the defense. It could also be indicative of a fundamental difference in the period that gave the attackers higher casualty rates than the defenders. This is an issue I would like to explore in more depth, and l may do so after l have more WWI data from the second validation.

Next: “Fanaticism” and casualties

Validating A Combat Model (Part IX)

Russian Army soldiers look over dead Japanese following the Battle of Port Arthur, February 1904. [Library of Congress]

[The article below is reprinted from April 1997 edition of The International TNDM Newsletter.]

The Second Test of the TNDM Battalion-Level Validations: Predicting Casualties
by Christopher A. Lawrence

Actually, l was pretty pleased with the first test of the TNDM, predicting winners and losers. I wasn’t too pleased with how it did with WWI, but was quite pleased with its prediction of post-WWII combat. But l knew from our previous analysis that we were going to have some problems with the casualty prediction estimates for WWI, for any battles that the Japanese were involved with, and for shorter engagements.

The problems in prediction of casualties, as related to certain nationalities, were discussed in Trevor Dupuy’s Numbers, Predictions and War: Using History to Evaluate Combat Factors and Predict the Outcome of Battles (Indianapolis; New York: The Bobbs-Merrill Co., 1979). In the original QJM, as published in Numbers, Predictions, & War, three special conditions served as attrition multipliers. These were:

  1. For period 1900-1945. Russian and Japanese rates are double those calculated.
  2. For period 1914-1941, rates as calculated must be doubled; for Russian, Turkish, and Balkan forces they must be quadrupled.
  3. For 1950-1953 rate as calculated will apply for UN forces (other than ROK): for ROK. North Koreans, and Chinese rates are doubled.

The attrition calculation for the TNDM is different from that used in the QJM. Actually the attrition calculations for the later versions of the QJM differ from the earlier versions. The base casualty rates that are used in the original QJM are very different from those used in the TNDM. See my articles in the TNDM Newsletter, Volume 1, Issue 3. Basically the QJM starts with a based factor of 2.8% for attackers versus 4% for the TNDM, while its base factor for defenders is 1.5% versus 6% for the TNDM.

When Dave Bongard did the first TNDM runs for this validation effort, he automatically added in an attrition multiplier of 4 for all the WWI battles. This undocumented methodology was implemented by Mr. Bongard instinctively because he knew from experience that you need to multiply the attrition rates by 4 for WWI battles. I decided to let it stand and see how it measured up during the validation.

We then made our two model runs for each validation, first without the CEV, and a second run with the CEV incorporated. I believe the CEV results from this methodology are explained in the previous article on winners and losers.

At the top of the next column is a comparison of the attacker losses versus the losses predicted by the model (graphs 1 and 2). This is in two scales, so you can see the details of the data.

The diagonal line across these graphs and across the next seven graphs is the “perfect prediction” line, with any point on that line being perfectly predicted. The closer a point is to that line, the better the prediction. Points to the left of that line is where the model over-predicted casualties, while the points to the right is where the model under-predicted. We also ran the model using the CEV as predicted by the model. This “revised prediction” is shown in the next graph (see graphs 3 and 4). We also have done the same comparison of total casualties for the defender (see graphs 5 through 8).

The model is clearly showing a tendency to under-predict. This is shown in the next set of graphs, where we divided the predicted casualties by the actual casualties. Values less than one are under-predictions. That means everything below the horizontal line shown on the graph (graph 9) is under-predicted. The same tests were done the “revised prediction“ (meaning with CEV) for the attacker and the both predictions for the defender (graphs 10-12).

I then attempted to do some work using the total casualty figures, followed by a series of meaningless tests of the data based upon force size. Force sizes range widely, and the size of forces committed to battle has a significant impact on the total losses. Therefore, to get anything useful, l really needed to look at percent of losses, not gross losses. These are displayed in the next 6 graphs (graphs 13-18).

Comparing our two outputs (model prediction without CEV incorporated and model prediction with CEV incorporated) to the 76 historical engagements gives the following disappointing results:

The standard deviation was measured by taking each predicted result, subtracting from it the actual result squaring it, summing all 76 cases, dividing by 76, and taking the square root. (see sidebar A Little Basic Statistics below.)

First and foremost, the model was under-predicting by a factor of almost two. Furthermore it was running high standard deviations. This last result did not surprise me considering the nature of the battalion-level combat.

The addition of the CEVs did not significantly change the casualties. This is because in the attrition equations, the conditions of the battlefield play an important part in determining casualties. People in the past have claimed that the CEVs were some type of fudge factor. If that is the case, then it is a damned lousy fudge factor. If the TNDM is getting a good prediction on casualties, it is not because of a CEV “fudge factor.”

SIDEBAR: A Little Basic Statistics

The mean is 5.75 for the attacker and 17.93 for the defender, the standard deviation is 10.73 for the attacker and 27.49 for the defender. The number of examples is 76, the degree of freedom is 75. Therefore the confidence intervals are:

With the actual average being 9.50, we are clearly predicting too low.

With the actual average being 26.59, we are again clearly predicting too low.

Next: Time and casualty rates

What Did James Mattis Mean by “Lethality?”

Then-Lt. Gen. James Mattis, commander of U.S. Marine Corps Forces, Central Command, speaks to Marines with Marine Wing Support Group 27, in Al Asad, Iraq, in May 2006. [Photo: Cpl. Zachary Dyer]

Ever since publication of the U.S. National Defense Strategy by then-Secretary of Defense James Mattis’s Defense Department in early 2018 made the term “lethality” a foundational principle, there has been an open-ended discussion as to what the term actually means.

In his recent memoir, co-written with Bing West, Call Sign Chaos: Learning to Lead (Random House, 2019), Mattis offered his own definition of lethality. Sort of.

At the beginning of Chapter 17 (pages 235-236), he wrote (emphasis added):

LETHALITY AS THE METRIC

History presents many examples of militaries that forgot that their purpose was to fight and win. So long as we live in an imperfect world, one containing enemies of democracy, we will need a military strictly committed to combat-effectiveness. Our liberal democracy must be protected by a bodyguard of lethal warriors, organized, trained, and equipped to dominate in battle. …

The need for lethality must be the measuring stick against which we evaluate the efficacy of our military. By aligning the entire military enterprise—recruiting, training, educating, equipping, and promoting—to the goal of compounding lethality, we best deter adversaries, or if conflict occurs, win at lowest cost to our troops’ lives. …

While not defining lethality explicitly, it would appear that Mattis equates it with “combat-effectiveness,” which he also does not explicitly define, but seems to mean as the ability “to dominate in battle.” It would seem that Mattis understands lethality not as the destructive quality of a weapon or weapon system, but as the performance of troops in combat.

More than once he also refers to lethality as a metric, which suggests that it can be quantified and measured, perhaps in terms of organization, training, and equipment. It is likely Mattis would object to that interpretation, however, given his hostility to Effects Based Operations (EBO), as implemented by U.S. Joint Forces Command, before he banned the concept from joint doctrine in 2008, as he related on pages 179-181 in Call Sign Chaos.