[The article below is reprinted from December 1996 edition of The International TNDM Newsletter. It was referenced in the recent series of posts addressing the battalion-level validation of Trevor Dupuy’s Tactical Numerical Deterministic Model (TNDM).]
Time and the TNDM
by Christopher A. Lawrence
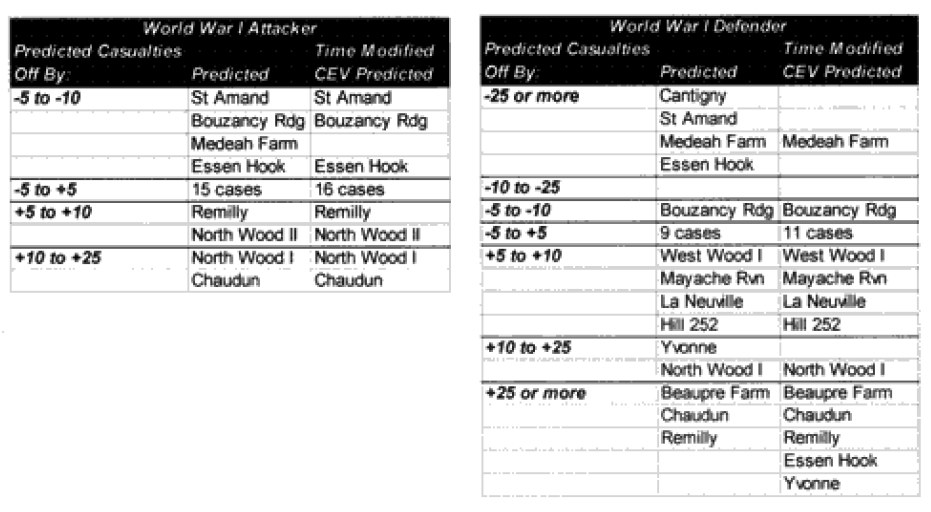
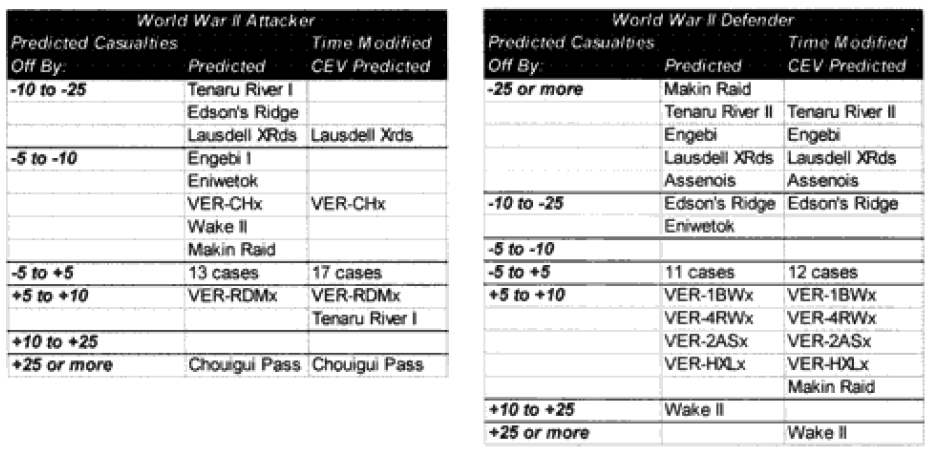
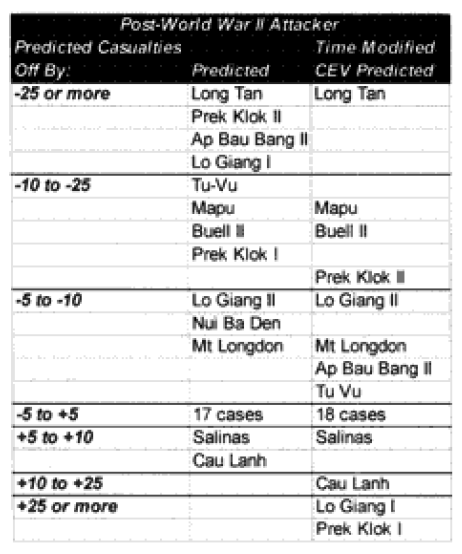
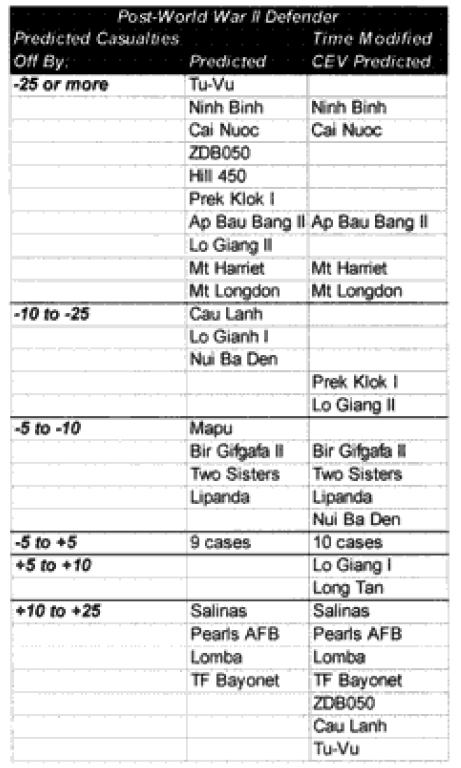
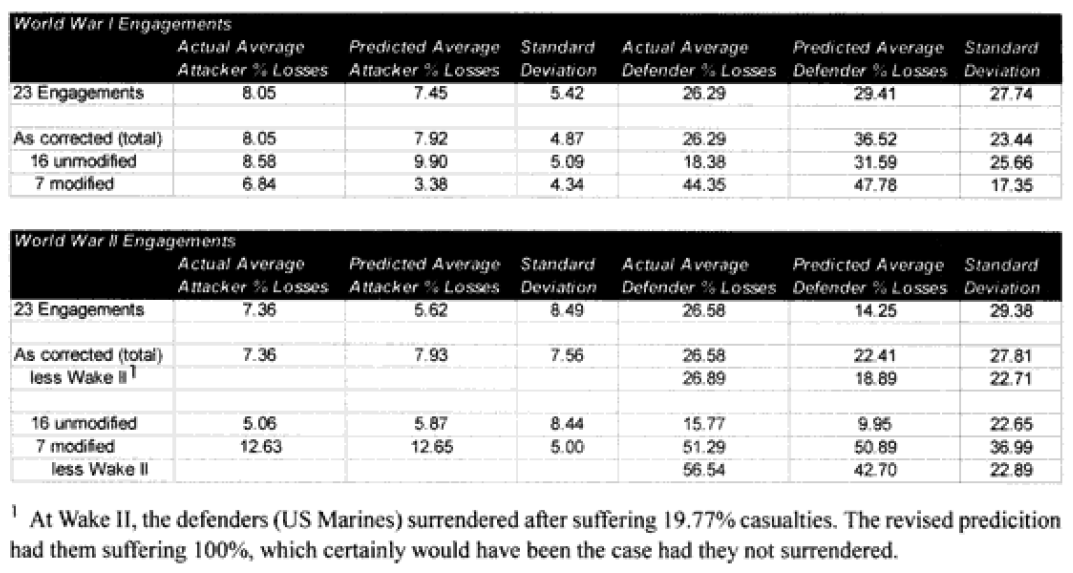
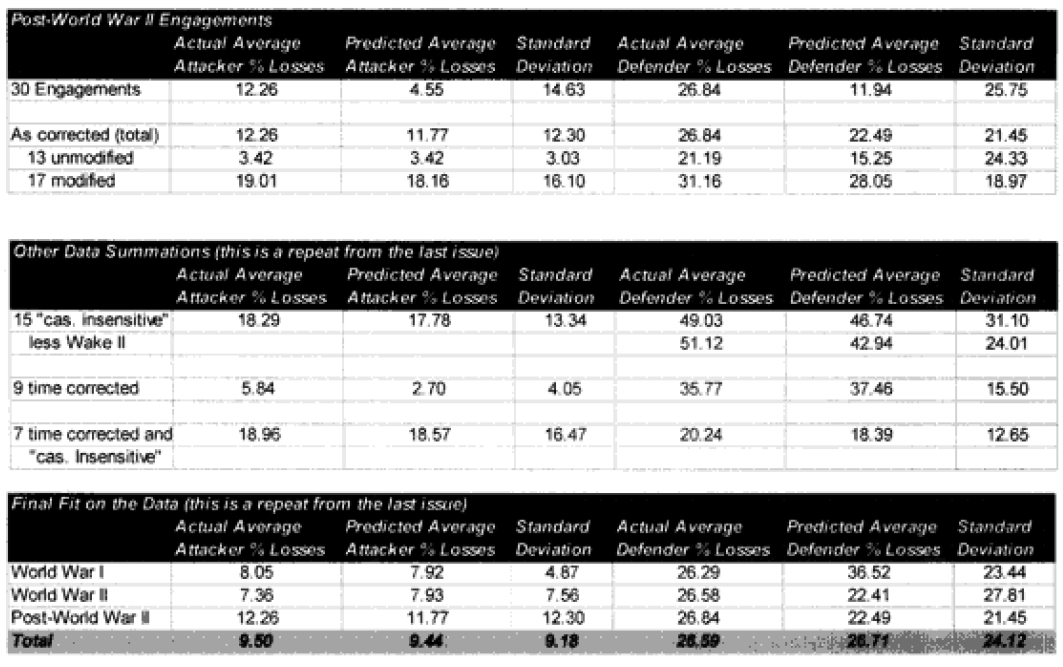
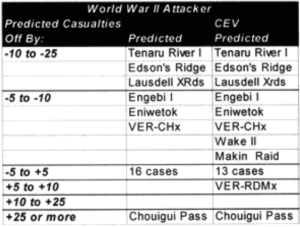
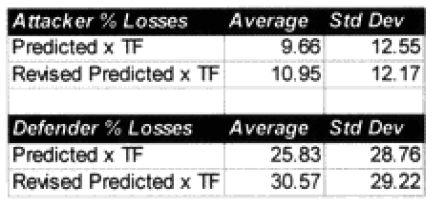
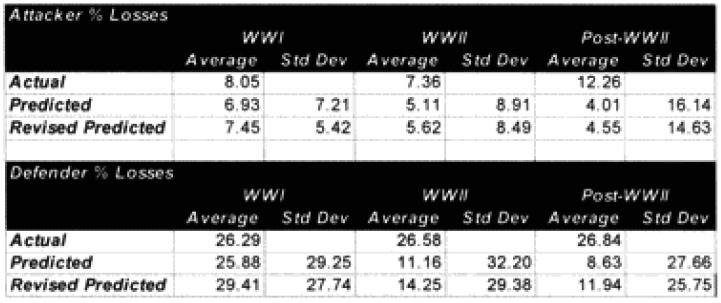
Combat models are designed to operate within their design parameters, but sometimes we forget what those are. A model can only be expected to perform well in those areas for which it was designed in and those areas where it has been tested (meaning validated). Since most of the combat models used in the US Department of Defense have not been validated, this leaves open the question as to what their parameters might be. In the cue of the TNDM, if the model is not giving a reasonable result, then you must ask, is it because the model is being operated outside of its parameters? The parameters of the model are pretty well defined by the 149 engagements of the QJM Database to which it was validated.
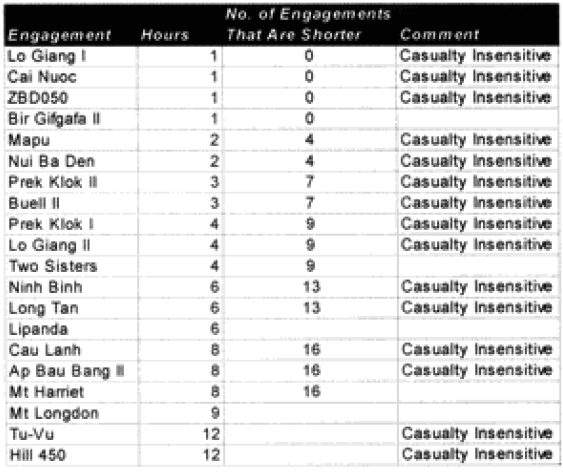
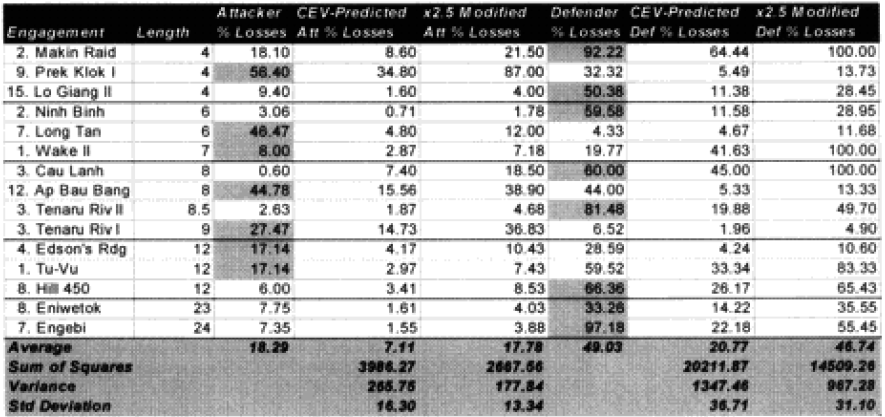
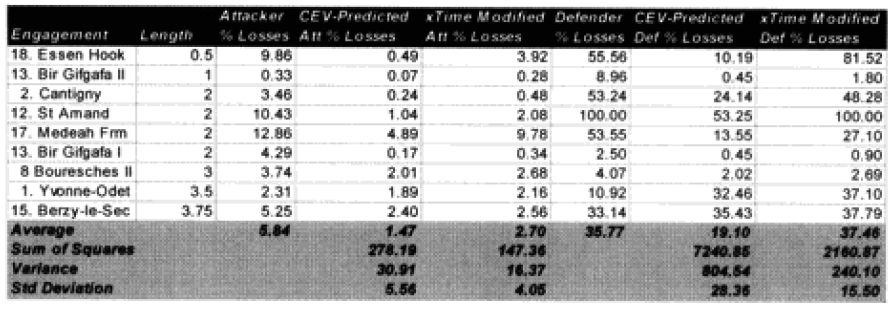
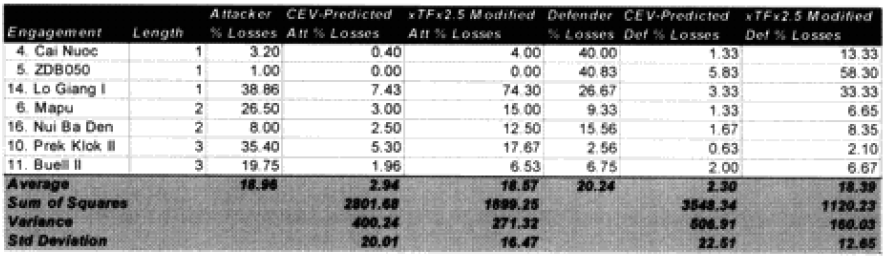
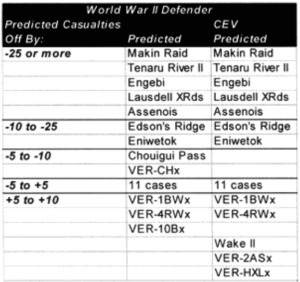
One of the areas where there is a problem with the TNDM is that while the analyst is capable of running a battle over any time period, the model was fundamentally validated to run 1 to 3 days engagements. This means that there should be a reduced confidence in the results of any engagement of less than 24 hours or over three days. The actual number of days used for each engagement in the original QJM data base is shown below:

 By comparison, the 75 battalion level engagements that we are using to validate the TNDM for battalion-level engagements occur over the following time periods:
By comparison, the 75 battalion level engagements that we are using to validate the TNDM for battalion-level engagements occur over the following time periods:
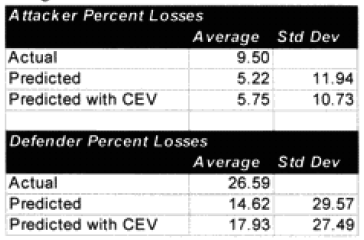
 Three of the engagements used in the battalion-level validation are from the QJM database.
Three of the engagements used in the battalion-level validation are from the QJM database.
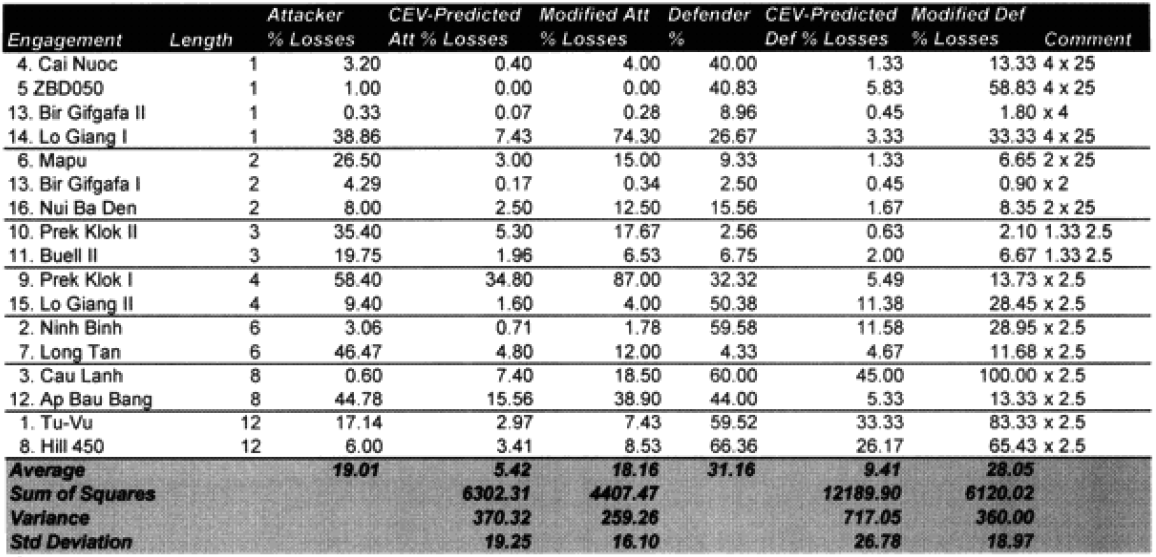
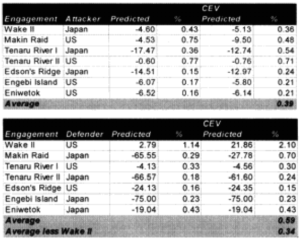
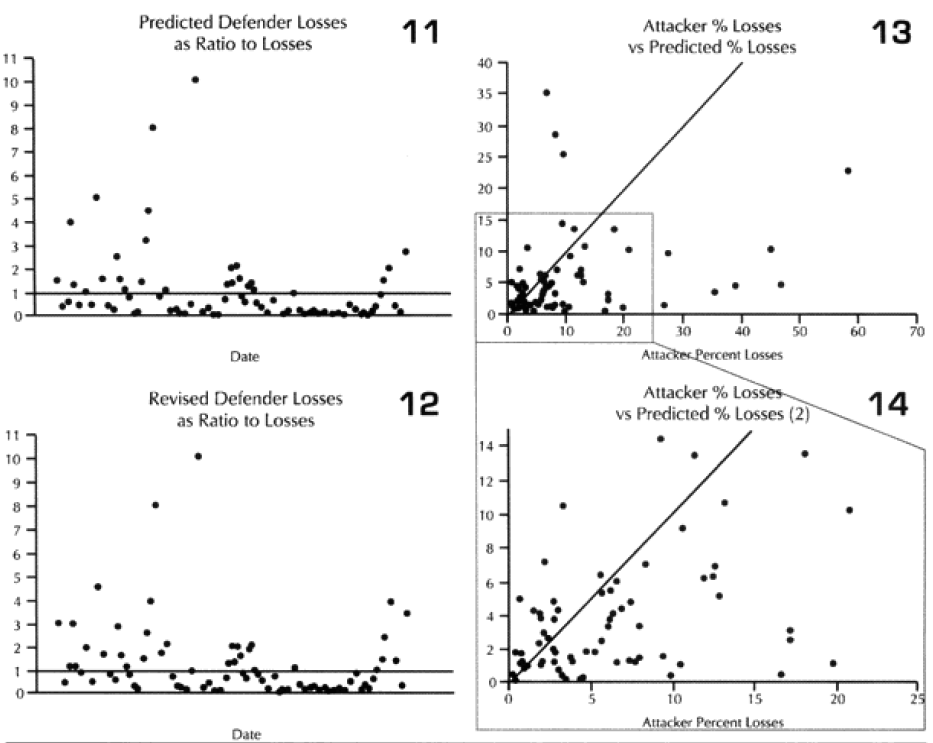
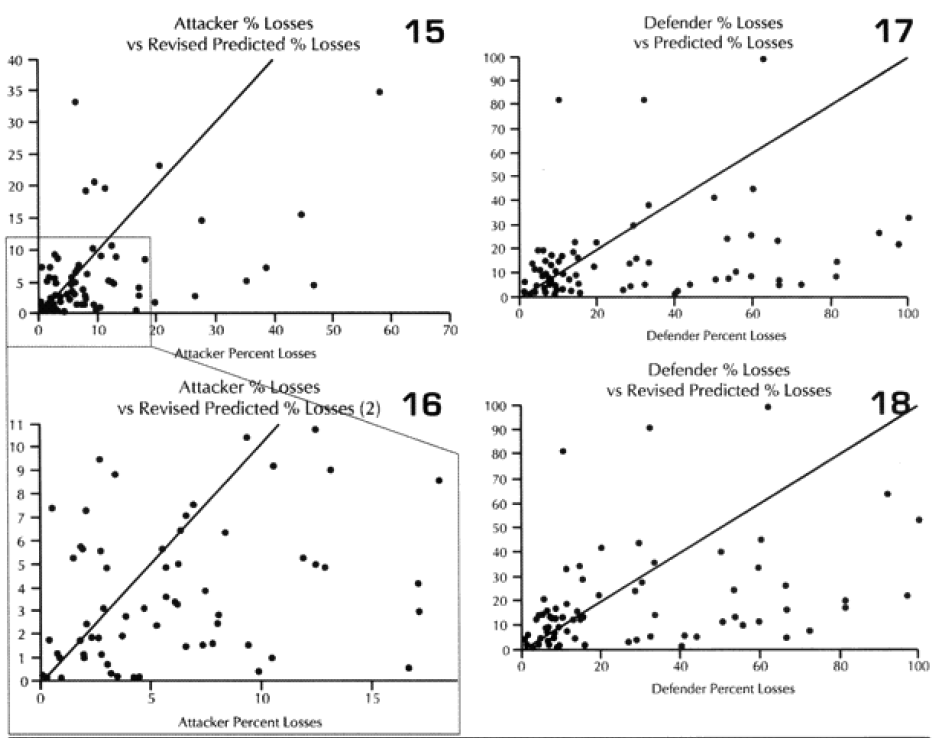
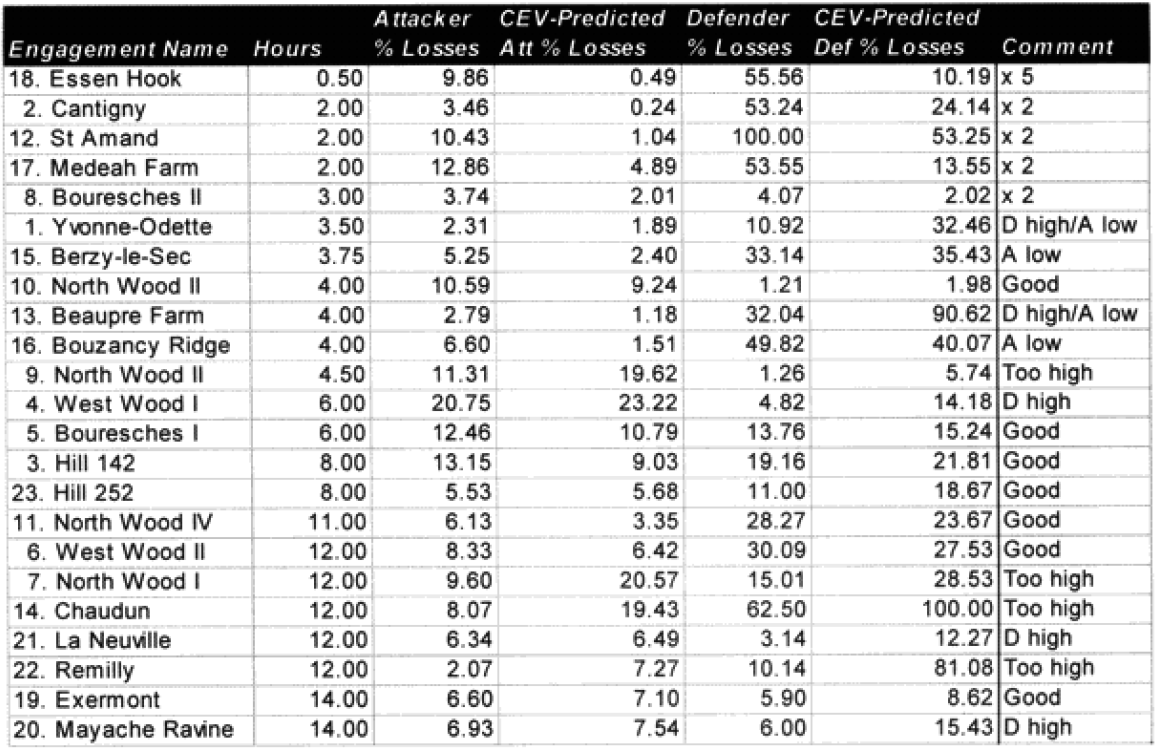
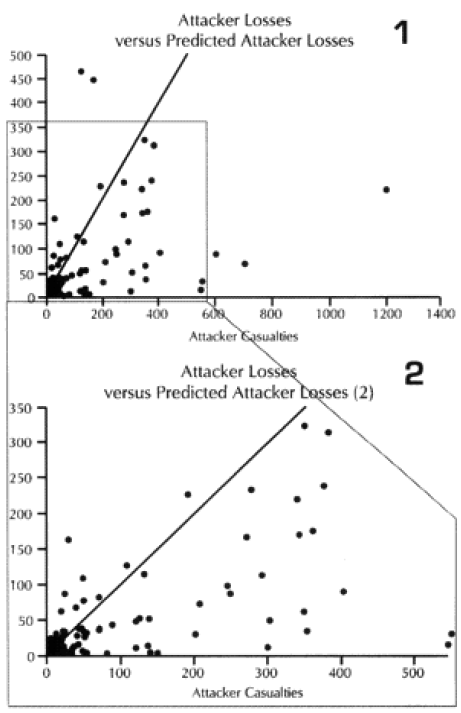
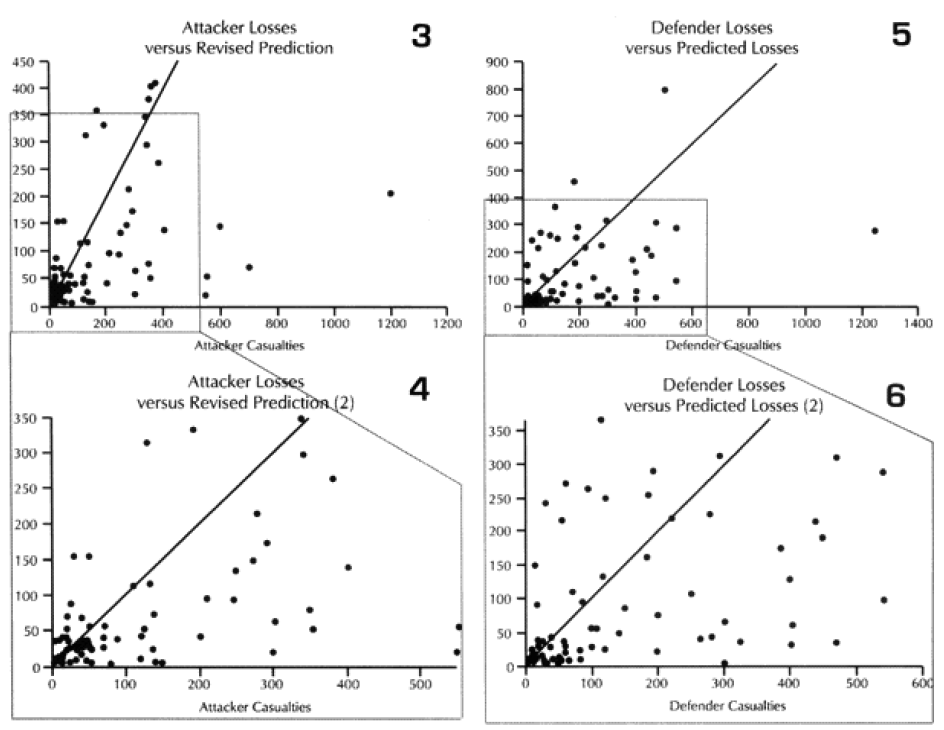
We did run sample engagements of 24 hours, 12 hours, 6 hours and 3 hours. The results of the 12-hour run was literally 1/2 the casualties and 1/2 of the advance for the 24-hour run. The same straight dividing effect was true for the 3- and 6-hour runs. For increments less than 24 hours the model just divided the results by the number of hours. As Dave Bongard pointed out to me, there are various lighting choices, including daylight and night, and these could vary the results some if used. But the impact for daylight would be 1.1 additional casualties and the reduction for night is .7 or .8.
The problem is that briefer battles will result in higher casualties per hour than extended battles. Also, in any extended battle, there are intense periods and un-intense periods, with the model giving the average result of those periods. For battles of less than 24 hours, there tends to be only intense periods. Therefore, it should be expected that battles lasting 3 hours should have more than 1/6 the losses of a 24 hours battle. This will be tested during the battalion-level validation.
For battles in excess of one day, there is a table in the TNDM that reduces the overall casualties and advance rate over time to account for fatigue.